Keplers Eklipsen-Instrument
Johannes Keplers Eklipsen-Instrument und sein
Beitrag zur Optik
Anjuschka Prenzel*
Kepler – ein philosophischer Mathematiker, der die Optik ins rechte Licht
rückt
Wer sich mit Kepler befassen möchte, kommt so schnell
nicht mehr von ihm los. Erstens hat er viele Bände gefüllt und zweitens nimmt
er durch seine präzise und feinfühlige Denkweise den Leser sofort gefangen, das
Gesagte zu überdenken. Für uns heutige ist alles klar, wenn wir etwas nicht
wissen haben wir Bücher und Internet und bekommen fast alles erklärt. Doch
hinterfragen wir es so tiefgründig wie Kepler? Er schrieb leidenschaftlich
gerne Briefe. Und wenn er keinen Adressaten hatte, richtete er sie an einen
Unbekannten, damit er loswerden konnte, was nicht in eine andere Abhandlung
passte. Das Schöne daran ist, dass wir dadurch viel über sein persönliches
Leben erfahren, seine sensiblen Gedanken, seine wirtschaftliche Situation,
seine Denkweise und seine Akribie. Auf jeden Fall steht fest, dass Kepler nicht
nur ein sturer Mathematiker war, sondern auch praktisch mit Instrumenten,
Linsen und Fernrohren experimentiert hat. Er versuchte seine
Forschungsergebnisse über die Strahlenoptik auch in der Praxis anzuwenden und
konstruierte beispielsweise ein Eklipsen-Instrument. Er wollte eine
Sonnenfinsternis mit Hilfe einer Lochkamera sichtbar machen. Dafür baute er ein
aufwendiges Gestell von fast 4 m im Quadrat – sein Finsternis-Instrument.
Damit beobachtete Kepler 1600 die Sonnenfinsternis in
Graz. Dabei interessierte ihn besonders, wie sich dabei der Mond verhielt. [1]
1. Wie sieht Kepler das „rechte Licht“?
Kepler kam an die Grenzen der geometrischen Optik und
entwickelte nun eine Lichttheorie. Im Band II der Gesammelten Werke „Astronomiae
pars optica“ Keplers, finden wir in „Paralipomena in vitellionem“ seine
kernigen Aussagen, die unserer heutigen Theorie den Weg bereitet haben. Im
Kapitel 1 „De natvra lvcis“, von der Natur des Lichts, sind im Anhang APPENDIX
AD CAPuT PRIMuM: ET VENTILATIO ARGVMENTORVM ARISTOTELIS DE VISIONE, Anhang zum
ersten Kapitel: Und bringt Ordnung in die Argumente der aristotelischen
Sichtweise vom Sehen, 21 Knackpunkte der neuen Denkweise aufgeführt. Hier setzt
er sich mit Aristoteles auseinander. [1] Da von diesen Aussagen keine
Übersetzungen vorliegen, habe ich mich selbst daran gemacht.
1. Color propriè et seipso fit
visus subiectum, et habet in seipso causam cur 20 visibilis existat.
Die Farbeigenschaft, die sichtbar zu sehen ist, hat in
sich selbst den Grund, warum sie existiert. Und wurde richtig dargestellt (von
Aristoteles, Anm. d. A.).
2. Lux est
actus perspicui quatenus perspicuum.
Die Ausdehnung des Lichtes ist transparent.
3. Est
quasi proprius quidam ipsius perspicui color, cum idverè perspicuum est.
Gewissermaßen ist die Eigenschaft der transparenten Farbe,
dass sie gebündelt ist.
(Also wusste er über das Lichtspektrum Bescheid, nicht
erst Newton. Anm. d. A.)
4. Non est
ignis, neque corpus, neque defluxus à corpore, sed est praesentia ignis aut
lucentis etc. in perspicuo.
Es ist nicht Feuer aus einem Körper noch Strömung aus
einem Körper, aber die Verbindung von Feuer und Licht, was einleuchtend ist.
5. Est
praesentia in corpore habitus eius, ob quem id perspicuum dicitur.
Es ist in der Weise vorhanden, dass es transparent ist.
6. Atque
haec ita capienda sunt, vt intelligamus, obloqui ARISTOTELEM EMPEDOCLI, qui
dixerat, ferri lucem tendique rectis lineis inter Terram et, quod nos ambit
atque complectitur (coelum), etsi à nobis non animaduertatur id fieri.
Und all diese Dinge werden wir besser umfassen und
verstehen, abgelehnt von Aristoteles und Empedocles, wie gesagt, durch die uns
umgebenden Lichtstrahlen in direkten Linien
vom Himmel zur Erde.
7. Eadem natura corporis est, quae iam lux est, iam
tenebrae.
Es ist der gleiche natürliche Körper, was jetzt Licht ist,
ist schon Dunkelheit.
(Also wir blicken in die
Vergangenheit! Diese Aussage halte ich persönlich für die wichtigste
Erkenntnis, die Kepler erhalten hatte. Anm. d. A.)
8. Et cum
id corpus potentia perspicuum est, tunc ibi tenebrae obtinent.
Bei völliger Transparenz des Körpers erhalten wir die
Finsternis.
9. Itaque
non cum actu perspicuum est, sed cum potestate, tunc igitur est et tenebrosum
et colorum capax, vtique quia tunc solùm est sine colore.
Daher ist die Transparenz nicht wirksam, weil sie ohne
Farbe ist.
10. Idem
et de planè non visis, et de iis quae aegrè conspiciuntur, affirmatur, quod
capacia sint coloris.
Und zwar
wirklich nicht zu sehen, also beinahe nicht sichtbar, sie ist weiß.
11. Est
autem id, quod actu perspicuum est, inter visibilia habendum, non verò seipso,
sed per colorem alienum et extraneum.
Unter den sichtbaren Objekten ist es (das Licht Anm. d.
A.) nicht wirklich getrennt, aber die
einzelnen äußerlichen Farben.
12. Fit
autem visio (seu visione natura prior motio, quam ego illustrationem oculi
dicerem) in hunc modum. Color mouet id quod est actu perspicuum, vt aerem, ab
hoc verò sic moto, quia continuum corpus est, vicissim mouetur et visus
instrumentum, seu oculus.
Das Sehen
geschieht in folgender Weise, d.h. das Sehen als Erleuchtung der Augen. Farbe
bewirkt in der transparenten Luft, dass der Körper unmittelbar gesehen wird
durch das Auge.
(Auch eine bahnbrechende Aussage, das Sehen erfolgt durch Lichtstrahlen,
die vom betrachteten Gegenstand ausgehen und nicht vom Auge. Anm. d. A.)
13. Atque
haec vna species est visionis, dum color scilicet videtur, in luce scilicet,
nunquam seorsim, quia lux est energia perspicui.
Während
Farbe freilich im Licht zu sehen ist, weil Licht transparent ist, ist die Farbe
nie von selbst zu sehen.
(Super – ohne Licht keine Farben! Anm. d. A.)
14. Itaque
fit visio (motio instrumenti quam sequitur visio) cum sensorium instrumentum
aliquid ab intermedio patitur.
Somit ist das Sehen (Wirkungsinstrument sowie Sichtfolge)
das sensorische Zwischenwerkzeug um das zu ermöglichen.
15. Neque
enim patitur aliquid oculus (non mouetur inquam, aut alteratur paries oculi) ab
ipso, qui videtur, colore.
Das Auge oder die Augenwand verändert nicht was gesehen
wird, nämlich Farben.
16.
Adeoque si spatium intermedium contingeret relinqui vacuum corpore, nihil
videri posset.
Ist der Körper in einem leeren Vakuum, so ist nichts zu
sehen.
17.
Analogia enim est inter visum, auditum et odoratum, ratione intermedii.
Analog dazu ist das Verhältnis zwischen dem Sehen und dem
Hören und Riechen.
18. Est
autem et alia species visionis, qua non colorem sed alia cernimus. Quo nomine
igni et Soli inest vnum et idem quippiam.
Die Sonne und
ihr Scheinen ist ein und dasselbe, aber wir sehen ihre Farbe nicht.
(Außerhalb der Atmosphäre ist die Sonne weiß. Kepler
vermutet dieses Weiß, was ich kolossal finde. Anm. d. A.)
19. Neque
omnia in luce cernuntur, sed aliqua et in tenebris efficiunt sensionem (seu
praecedentem hanc motum instrumenti).
Ebenso
wenig das wahrgenommenen Licht, aber irgendwie und in Dunkel gehüllt
wahrgenommen.
(Kepler merkt, dass das Licht etwas in sich verbirgt. Anm.
d. A.)
20. Nam
etiam ab igne perspicuum (in potentia) fit perspicuum (actu).
Denn auch der helle Glanz ist transparent.
21. Et
quae noctu seu in tenebris cernuntur, eorum aliqua splendent quidem, lucem verò
non ingerunt.
Das heißt, in der Nacht oder in Finsternis glitzert es und
das Licht ist wahrhaftig nicht dunkel.
An Keplers Sätzen kann ich mich nicht sattlesen. Seine
Betrachtungsweise erweckt auch heute eine völlig neue Sicht auf das was man
Physik nennt. Vielleicht müssen wir wieder so denken lernen um etwas völlig
Neues zu entdecken, was unser Leben von Grund auf zum Positiven verändert.
2. Keplers Finsternis-Instrument
Zu den Erläuterungen dieses Gerätes fand ich keine
Übersetzung und deshalb habe ich mich selbst daran versucht, wie im
vorhergehenden Kapitel. So großzügig wie er sonst seine geometrische Optik
darstellte, war er bei der Beschreibung seiner Konstruktion allerdings nicht.
Aus seiner 3D-Zeichnung kann aber einiges erkannt werden, damit seine Worte
verständlich werden. Keplers „Astronomiae pars Optica“ [1] ist faszinierend.
Dort habe ich mir das Eklipsen-Instrument herausgepickt und wollte nicht
aufhören, bis ich hinter seine „Schliche“ gekommen bin. Da ich im Besitz dieses
Bandes bin, Band II der Gesammelten Werke, konnte ich gründlich arbeiten. Für
Latein-Fans hier der Text: Auf Seite 288 geht es los.
2.1. Keplers Beschreibung seines Bausatzes
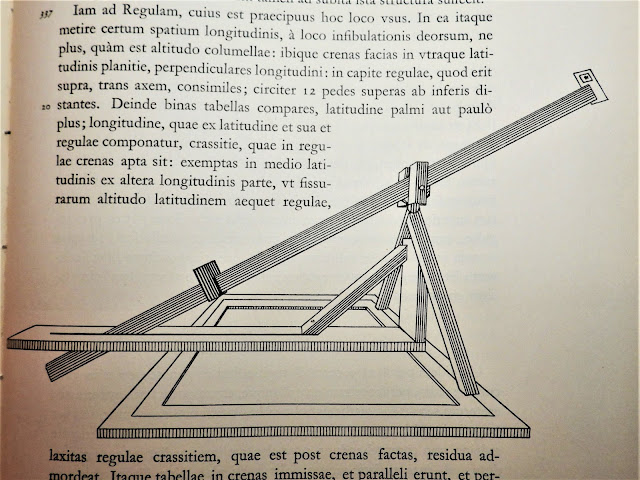
Bild 1. Eklipsen-Instrument nach Johannes
Kepler [1]
___________________________________________
Die Beobachtung der scheinbaren Durchmesser von Sonne
und Mond und der Finsternisse beider
Konstruktion eines Ekliptik-Instrumentes Kapitel XI in
Astronomiae pars Optica [1]
Hier ist erst einmal der Originaltext für Latein-Fans.
„Scena sub
dio erigatur, pannis nigris totuplicibus, ne quid lucis irrumpat.
Si haec
deest commoditas, conclaue eligatur obuersum in plagam, unde Solis defectus
spectabitur: sit huic conclaui paries non crassus, qui fenestram praebeat:
possitque cum haec fenestra tum omnes rimae obturari contra lucis ingressum.
Deinde
Regula fabrefiat quantae fieri potest longitudinis, cuius lineae omnes rectae
sint, crassities quantam asser dedolatus praebet, latitudo semipedis.
Ea sic
aptetur, vt quia flexile est lignum, in dorsum incumbat, et inter capita loco
intermedio, quò minus flectatur.
At neque
in medio latitudinis perforetur, ne imbecillius factum frangatur suo pondere.
Quin
potius ad lineam dorsi, cui incubiturum est, coassetur trabecula, vt in
coassationis linea centrum foraminis seu matriculae constitui possit.
Matriculae
suus axiculus sito.
Deinde
fiat columella versatilis super axe; in summo bifida, vt fissura crassitiem
regulae excipere; perforata, vt eodem cum regula axiculo traiici possit.
Deinde
fiat columella versatilis super axe; in summo bifida, vt fissura crassitiem
regulae excipere; perforata, vt eodem cum regula axiculo traiici possit.
Trabecula
in qua matricula columellam excipiens, tignis aequalibus, hinc inde transuersim
surgentibus columellam in sui (trabeculae) perpendiculo statuant, cauo complexu
columellam teretem in sublimi includentes.
Huic
trabeculae tres aliae socientur, vt ex omnibus fiat parallelogrammum
rectangulum, loco circuli Azimuthalis.
Capiti
verò columnae, à quo axis in trabeculam exit, committatur et coassetur
transtrum in earum planitierum columellae altera, quae fissuram habet supra, et
confibuletur hoc quoque transtrum columellae transuersali, vt recto angulo
columella transtro cohaereat; et transtrum parallelogrammo incumbens si
moueatur, columellam conuertat.
Transtrum
longitudine sit idonea, in medio exempta, vt crassitiem regulae hac fissura
capiat, regulaque cum transtro et columella circumferatur: simulque regula
versus verticem erigi, aut versus horizontem demitti possit, quantum Solis
altitudo sub principium et finem Eclipseos postulat.
Propterea
et columellam tam altam esse conuenit, vt parallelogrammum regulam nuspiam
impediat, et transtrum tàm longum, ipsamque regulam, ne sese deserant, Sole
cadente; fissurasque vtrobique eodem aptatas, ipsumque quadratum sublime, ne
regula depressa pauimento occurrat: et in plano horizontis, quod columellae
appensum perpendiculum facilè indicabit.
Neque sanè
vniuersalis esse potest haec forma, nisi aut ex transtro et columella fiat
quadratum geometricum, aut omninò quadrans adhibeatur.
In ea
itaque metire certum spatium longitudinis, à loco infibulationis deorsum, ne
plus, quàm est altitudo columellae: ibique crenas facias in utraque latitudinis
planitie, perpendiculares longitudini: in capite regulae, quod erit supra,
trans axem, consimiles; circiter 12 pedes superas ab inferis distantes.
Deinde
binas tabellas compares, latitudine palmi aut paulò plus; longitudine, quae ex
latitudine et sua et regulae componatur, crassitie, quae in regulae crenas apta
sit: exemptas in medio latitudinis ex altera longitudinis parte, vt fissurarum
altitudo latitudinem aequet regulae, laxitas regulae crassitiem, quae est post
crenas factas, residua admordeat.
Itaque
tabellae in crenas immissae, et paralleli erunt, et perpendiculares regulae in
longum et latum.
Ducatur in
vtraque tabella linea per longitudinem, consurgens à medio fissurae et
crassitiei regulae, eique bisectae in puncto sectionis alia erigatur ad
perpendiculum, per totam latitudinem tabellae ducta.
Post in
altera tabella, quae superior futura, partes medias, in quibus erat rectarum
sectio, fenestra quadranguIa duorum digitorum latitudine eximas, maneant verò
in margine fenestrae, residua rectarum.
In lamina
verò aenea tenuissima, benè complanata, nec contumaci, binae lineae sese secent
ad rectos: et sectione centro, circellus fiat pisi magnitudine, vt minor sit
haec diameter ad distantiam tabellarum, quàm diametri luminarium ad suas
distantias, per 6. secundi capitis; pertundaturque, vt foramen accuratè
circulare sit, interque decussatas lineas medium: latitudo laminae paulò maior
fenestella.
Haec affigatur
tabellae perforatae, vt lineae in lineas quadrent, et foramen in meditullio
fenestellae constituatur. In altera tabella, quae futura est inferior et
planitie sursum versa, ex centro sectione linearum, describe circulum, quantum
fert latitudo tabellae, diuisum à summa ad partes medias, in gradus 90
singulos, totidemque vtrinque ab imo. Aut si placet, vtere alia numerorum
serie.
Deinde
tabella capiat in medio stylum breuissimum in centro seu sectione.
Circa hunc
volubilis aptetur rotula, in qua postmodum circellos ex puncto affixionis sumus
descripturi.
Ex altera
parte rotulae pro mineat index, cuius extrema linea ex centro rotulae exeat,
longitudine tanta, vt in circulum tabellae pertingat, et rotulae conuersione
index in hoc circulo circumferatur.
Quibus sic
constructis, dimetire omnia subtilissimè, vt in meo instrumento feci.
Vbi ad
vsum ventum erit, canali intus nigro iter tabellis interiectum vela, sic vt
nuspiam luci pateat hoc circulo circumferatur ingressus nisi per fenestellam
superioris tabellae: instrumentum verò sic colloces, vt ea pars regulae, quae
supra columellam est, cum canali et tabella foris sit extra scenam in aperto
aere, reliquum intra in tenebris, possitque liberè conuerti.
Et sit fenestra, quae regulam foras emittit in aerem, benè
circumcirca communita contra lucem.“
Jetzt folgt meine Übersetzung
Ein Rahmen wird unter freiem Himmel möglichst total in
schwarzes Tuch eingewickelt, damit sich das Licht nicht bricht.
Es ist vorteilhaft die Richtung nach Westen zu nehmen, wo
die Sonne nur betrachtet werden kann: der abgeschlossene Raum ist nicht dicht,
eine Wand bietet ein Fenster: bei diesem Fenster und allen winzigen Ritzen ist
der Lichteintritt zu verhindern.
Dann wird das Schienengestell längs möglich eingefügt, die
Dicke der Bretter ist ein halb Zoll (1,27 cm) breit.
Es wird so angepasst, dass ein Stück Holz als Rückenstütze
dient zwischen der Lücke, ansonsten entsteht eine Verbiegung.
Um nicht durch sein Eigengewicht zerdrückt zu werden,
wurde sie in der Breite durchbrochen.
Der kleine Balken
liegt auf dem Rücken des
Bretterbodens auf, z.B. auf dem äußeren Umriss, oder um die Lage der mittleren
Spalte zu bestimmen.
Begrenzt das Aufliegen.
Der Spalt ermöglicht eine Bewegung der Achse; sodass der
Spalt die Dicke der Latte aufnimmt, welche perforiert ist und durch eine kleine
Bohle gehalten wird.
Das Gefüge liegt auf.
Der Spalt ist so beschaffen, dass eine leichte
Drehbewegung möglich ist; so perforiert, dass die Latte in der gleichen Lage
der Achse liegt.
Der kleine Balken im Apparat der die Säule stützt, der
gleiche Balken, von da an überträgt die emporgerichtete Stütze schnurgerade das
Bild, vorausgesetzt ist die völlig glatte Höhlung für die Säule.
Es besteht das Risiko ein Parallelogramm zu erhalten
anstelle von Azimuth-Kreisen.
Der Kopf des Pfostens, ausgehend von der Achse, ist
vollends mit dem Kehlbalken und dem bretternen Boden verbunden, in seiner Ebene
der andere Pfosten, der Ritz führt drüber heraus, dieser Kehlbalken durchsticht
den Pfosten, dass der rechtwinklige Balken verbunden bleibt mit dem Kehlbalken;
und der parallele Kehlbalken stützt bei Bewegung des Balkens.
Beim Kehlbalken kann die Mitte herausgenommen werden, also
die dicke Latte, die den Aufnahmeschlitz hat, die Schiene zum Kehlbalken und
zum sich herumdrehenden Zapfen: ähnlich der entgegengesetzt aufgerichteten
Wendelatte, oder horizontal gewendet beim Herabsenken, so lange wie unter der verweilenden Finsternis die Eklipse
die Sonne bedeckt und die erwartete Sonne begrenzt.
Deswegen steigt die Säule so hoch wie angemessen, die
parallele Latte ist gestützt, und der Kehlbalken außerdem längs, die Leiste
nicht fallen lassen, wenn die Sonne sich senkt; der Schlitz ist in Stellung,
die festgemachte tiefe Latte nicht aufstoßen: und in horizontaler Ebene, weshalb
die hängende senkrechte Säule ohne Mühe
die Anzeige übermittelt.
Der Grundriss hat keine universale Wirkungswiese, wenn
nicht der Kehlbalken und die Säule ein geometrisches Quadrat bilden und
gänzlich quadratisch verbunden werden.
Dennoch wird sich die Struktur unerwartet darstellen.
Die schon vorgeschriebene Regel ist notwendig anzuwenden.
Damit sollte man sich um eine rechtwinklige Messung des
Raumes bemühen, ein Ort, unten dicht, höchstens die Höhe der Säule: sowohl in
der Breite der Ebene als auch senkrecht zur Länge: an der Schienenspitze über
der Achse ist es genauso; ungefähr 12 Fuß (3,6576 m) Abstand von oben nach
unten.
Von da an vergleichen sie die zwei kleinen Brettchen, mit
der Breite der Handfläche oder ein wenig mehr; die Maße gehen von der Breite
der dicken Latte aus: in der Mitte hat die Ritze die gleiche Höhenbreite wie
die Latte, die lockere dicke Schiene bleibt angelegt, wenn sie betätigt wurde.
So wird das Brettchen senkrecht auf die Latte aufgesetzt.
Die Führung auf
beiden Seiten des Brettchens ist längs der Linie, ein Mittelschlitz gemäß der
Lattendicke und halb so tief.
Danach ist eines, was sich künftig oben befindet in
gerader Linie, in einem quadratisches Fenster, zwei Finger breit davon, das im
Fensterrahmen bleibt.
Auf einen dünnen Blechstreifen, gut geglättet, oder
geebnet, aber auch nicht unbiegsam, kommen zwei gerade Linien: und im Zentrum
wird ein erbsengroßer Ring ausgeschnitten, dessen Durchmesser sich zum Abstand
des Brettchens wie der
Lichtöffnungsdurchmesser zu seinem Abstand verhält; wenn der Kreis des durchbohrten Loches
akkurat ist, kreuzen sich darunter die Mittellinien: das Ausmaß des
Blechstreifens ist nicht viel größer als das Fenster.
Dieses befestigte perforierte Brettchen, in Form eines
Quadrates, wird mit der Öffnung in den Mittelpunkt des kleinen Loches gesetzt.
Auf der anderen Seite des Brettchens, da wo die Projektionsebene hin und her
bewegt wird, nach dem Mittelpunkt des beschriebenen Lochkreises, hat die
Tischbreite eine Einteilung in 90 einzelne Grade. Oder verwenden sie andere
Zahlen.
Dann steckt man in das Zentrum des Brettchens einen kurzen
konischen Stift.
Dieser ist um sich herum drehbar, ein genau passendes
Rädchen, für den ausgeschnittenen erbsengroßen Kreis, der schon beschrieben wurde.
Dieser konische Zeiger, der in das Brettchen gesteckt
wurde, kann darin gedreht werden.
Wird diese Konstruktion gebaut, müssen alle Durchmesser
genau sein, wie in meinem Instrument.
Wenn das Brettchen in dem inneren Kanal
dazwischengeschoben wird, so wird nirgends ankommendes Licht eintreten als nur
durch ein Fenster oben am Bettchen: das Instrument ist so gestellt, dass das Lattengestell im Inneren in der
Dunkelheit steht, außen sollte in offener
Luft, möglichst ein freier Sichtkegel sein.
Das Fenster sollte außerhalb der Schiene gut ringsherum
gegen das Licht geschützt sein.
Ich habe mir erlaubt, auch so ein Gerät zu „bauen“ (Bild
2).
Bild 2. Das Keplersche Finsternis-Instrument
„nachgebaut“
______________________________________________
2.2. Veranschaulichung seiner Konstruktion
Im Prinzip ist es eine Lochkamera. Die
verfinsterte Sonne sollte sich auf einem Brettchen a darstellen, dass auf einer Schiene b befestigt wird. Die Schiene befindet sich in
einem Zelt von schwarzem, lichtundurchlässigem Tuch und geht durch ein gut
abgedichtetes Fenster, das durch ein Brett c mit sehr kleiner Öffnung verschlossen wird
heraus. Im Zelt vor diesem Brettchen c wird ein Blech d so befestigt, dass seine erbsengroße Öffnung
genau vor die kleine Öffnung des Brettchens c kommt. Das Blech hat eine Gradeinteilung. In dieses Loch wird ein
konischer Stift e gesteckt, der zu drehen geht und den Lichtstrahl
richten kann, das sogenannte Rädchen. Auf Keplers Zeichnung sieht dieser
Stift so aus, als hätte er einen bestimmten Kopf, der beim Drehen das Licht je
nach Graduierung hereinlassen kann und die andere Fläche abdunkelt, also ein
Rädchen, wie er es sagt, doch die Mitte von e muss ja auch perforiert sein. Vielleicht hat es
unterschiedliche Lochstärken? Mit der Gradeinteilung soll wahrscheinlich die
Sonnenfinsternis in ihrem Ablauf verfolgt werden können. Das schwarze Tuch mit
dem Fenster darf nicht gespannt sein, da der Apparat Bewegungen sowohl in
vertikaler als auch in horizontaler Richtung ermöglicht, um die Sonne verfolgen
zu können.
Es gibt ein interessantes Buch [3] in welchem die Formel
für einen optimalen Lochdurchmesser aufgeführt wird:
D= 1,6*sqrt(b*Lambda) (anders konnte ich es im Blog nicht schreiben!)
b - Bildweite zwischen Loch und Auffangebene (Bildebene)
Lambda - Wellenlänge (sichtbares Licht 400-675 nm)
Wenn wir bei einer Länge von 3,8 m auf der
Projektionsebene etwas deutlich sehen wollen, dann müsste der Lochdurchmesser
2,2 mm betragen.
Der ganze Aufbau von Keplers Kamera hat in Höhe, Länge und Breite die Abmessung
von ca. 12 Fuß, das sind also ungefähr 3,7 bis 4 m. Den Trick mit dem Rädchen
fand ich gut, so konnten die Lichtstrahlen fein eingestellt werden, denn
Nanometer waren noch nicht definiert.
Kepler – ein Genie
Keplers geniale Forschungen werden stets damit
überschattet, dass er das Brechungsgesetz nicht formulieren konnte. Doch
schauen wir uns doch seine Aussagen an, dann sehen wir, dass gerade er das
Licht in seiner Natur nicht zerteilt betrachtet, sondern im Sinne der
Quantenphysik. Für ihn gab es nur das Licht als etwas, das bestimmte Effekte
hervorruft. Das angebliche Genie Galilei hat natürlich Versuche zur Ermittlung
der Lichtgeschwindigkeit vermarktet, was ja Kepler sicher auch wusste. Kepler
war ein gestandener Mathematiker und wusste was Trigonometrie ist. Er wollte
aber nicht nur Strahlen zeichnen, sondern das Wesen des Lichts ergründen. Eine Lichtgeschwindigkeit zu definieren, lag
nicht im Ermessen seiner Zeit. Sicherlich hatte Kepler bei seiner gründlichen
Denkweise erst einmal genug damit zu tun, das Wesen des Lichtes zu definieren.
Es gab ja noch keinen Wellenbegriff und für einen Korpuskelbegriff war die Zeit
erst recht nicht reif. Liest man in seinen Texten, dann erschließt sich eine
Welt voller sensiblen Denkens über das Licht, was ist da schon ein Formel über
ein Gesetz, das auch nur annähern genau ist. Die Bewegung von Lichtstrahlen war
für ihn nicht nur ein Ereignis der Mechanik, was an seinen oben übersetzten
Aussagen zu sehen ist. Ein noch so ausgeklügelter Versuchsaufbau zur
Lichtgeschwindigkeitsmessung ersetzt nicht die Tragweite von Keplers
Gedankengängen.
Deshalb wundere ich mich immer darüber, dass es Leute
gibt, die an Keplers Verdiensten herumnörgeln und ihn halb als Versager
hinstellen. Er kannte doch sicher den Regenbogen und die Brechung des
Sonnenlichts am Prisma, z.B. wenn das Sonnenlicht sich am geschliffenen Rand
eines Spiegels farbig bricht. Der Gipfel ist, dass angebliche Wissenschaftler
seiner Zeit die Lichtgeschwindigkeit errechneten aber nicht veröffentlichten.
Dem Kepler haben sie das nur nicht verraten, so liest sich das dann. Mit seinem
Augenlicht wurde auch stets herumgeunkt. Wenn er so schlecht hätte sehen
können, wie war es denn dann möglich, ganze Bände zu füllen, Teleskope zu bauen
und Lochkameras zu bedienen. Ich sage euch, ohne Kepler hätte es auch keinen
Newton gegeben. Und warum ist auf dem Mond der kleinere Krater mit Kepler
benannt und der größere mit Kopernikus? Ich sage auch noch, der ganze Mond muss
„Kepler“ heißen.
Literatur
[1] Johannes Kepler Gesammelte Werke Band II, Astronomiae
pars optica, heraussgegeben von Franz Hammer, C.H. Beck’sche
Verlagsbuchhandlung, MCMXXXIX, 1939
[2] Ostwalds Klassiker der exakten Wissenschaften Band
198, Johannes Kepler, Schriften zur Optik 1604-1611, Rolf Riekher, Verlag Harri
Deutsch
[3] Das Photographische Objektiv, Johannes Flügge,
Springer-Verlag, Wien 1955
http://www.keplerraum.at/stadt.html
aufgerufen am 26.09.2019
aufgerufen am
30.05.2019
aufgerufen am 11.06.2019
https://en.wikipedia.org/wiki/Johannes_Kepler#Astronomiae_Pars_Optica
aufgerufen am 11.06.2019
http://publikationen.badw.de/de/002334738
aufgerufen am 11.06.2019
https://astrokramkiste.de/kepler
aufgerufen am 11.06.2019
https://cs.wikipedia.org/wiki/Johannes_Kepler
aufgerufen am 11.06.2019
aufgerufen am 11.06.2019
https://de.wikipedia.org/wiki/Johannes_Kepler#Dioptrice
aufgerufen am 11.06.2019
https://cs.wikipedia.org/wiki/Dioptrice
aufgerufen am 13.06.2019
http://www.gbv.de/dms/ilmenau/toc/569945577.PDF
Schriften
zur Optik
aufgerufen am 13.06.2019
https://books.google.de/books?hl=de&lr=&id=SniVDwAAQBAJ&oi=fnd&pg=PR5&dq=Messmethoden+der+Lichtgeschwindigkeit&ots=EoiWto3TwA&sig=ocH5_5YXX81oUSAkvuGyp2e7zRk#v=onepage&q=Lichtgeschwindigkeit&f=false
aufgerufen am 27.09.2019
Bitte verzeiht das schlechte Layout, es ist nicht meine Absicht!
Bitte verzeiht das schlechte Layout, es ist nicht meine Absicht!
Veröffentlicht im Jahrbuch Optik und Feinmechanik 2019
ISBN 978-3-00-064986 8
im OPTIK-Verlag Dr. Prenzel
www.optik-verlag.com


Kommentare
Kommentar veröffentlichen